Representacion Grafica De La Multiplicacion De Fracciones Para Niños – ¡Embárcate en un viaje fascinante con nuestra guía ilustrada sobre la representación gráfica de la multiplicación de fracciones! Diseñada especialmente para niños, esta guía transforma un concepto aparentemente complejo en una aventura visual que iluminará sus mentes.
Sumérgete en un mundo de fracciones donde los dibujos animados y los ejemplos de la vida real cobran vida, guiando a los jóvenes estudiantes a través de los pasos de la multiplicación de fracciones de una manera clara y atractiva.
Representación Visual de la Multiplicación de Fracciones: Representacion Grafica De La Multiplicacion De Fracciones Para Niños
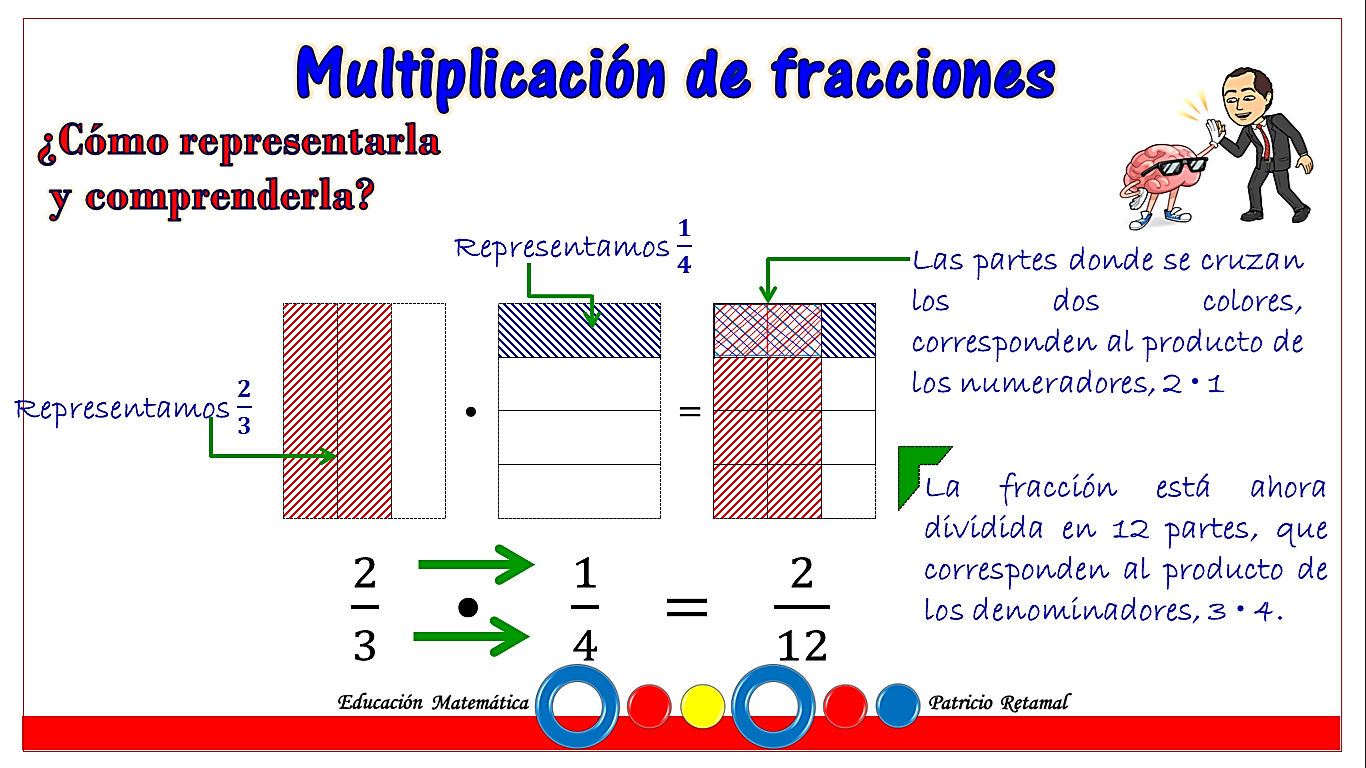
La multiplicación de fracciones es un concepto fundamental en matemáticas. Para ayudar a los niños a comprender este concepto, es esencial utilizar representaciones visuales que hagan que el proceso sea más tangible y fácil de entender.Una forma de representar visualmente la multiplicación de fracciones es utilizando una tabla.
La tabla debe tener cuatro columnas:
Tabla de Multiplicación de Fracciones
| Fracción 1 | Fracción 2 | Representación Visual | Resultado |
|---|---|---|---|
| 1/2 | 1/3 | 1/6 | |
| 3/4 | 1/2 | 3/8 | |
| 1 1/2 | 1/4 | 3/8 |
La tabla muestra cómo multiplicar fracciones simples y mixtas utilizando una representación visual. Las imágenes ayudan a los niños a visualizar el proceso y a comprender cómo se combinan las fracciones para formar un nuevo valor.
Multiplicación de Fracciones con Números Enteros

¡Bienvenidos, pequeños matemáticos! En esta aventura matemática, exploraremos el fascinante mundo de multiplicar fracciones con números enteros. Juntos, descubriremos cómo transformar estos números mágicos en productos asombrosos.
Multiplicando Fracciones por Números Enteros
Cuando multiplicamos una fracción por un número entero, el proceso es similar a multiplicar cualquier otro número. Echemos un vistazo a los pasos:
- Paso 1: Convierte el número entero a una fracción:Escribe el número entero como una fracción con denominador 1. Por ejemplo, el número entero 3 se convierte en la fracción 3/1.
- Paso 2: Multiplica los numeradores:Multiplica el numerador de la fracción por el numerador del número entero. Por ejemplo, si multiplicamos 1/2 por 3, multiplicamos 1 por 3 para obtener 3.
- Paso 3: Multiplica los denominadores:Multiplica el denominador de la fracción por el denominador del número entero. En nuestro ejemplo, multiplicamos 2 por 1 para obtener 2.
- Paso 4: Simplifica (si es posible):Si el resultado es una fracción impropia (numerador mayor que el denominador), conviértela en un número mixto o decimal.
Ejemplo
Multipliquemos 1/2 por 3:
- Convierte 3 a una fracción: 3/1
- Multiplica los numeradores: 1 x 3 = 3
- Multiplica los denominadores: 2 x 1 = 2
- El resultado es 3/2, que es una fracción impropia. Simplificándola, obtenemos 1 1/2.
¡Y así, hemos multiplicado una fracción por un número entero con facilidad! Ahora, ¡sigamos explorando juntos este maravilloso mundo de las matemáticas!
Multiplicación de Fracciones con Decimales

Multiplicar fracciones por decimales es un proceso sencillo que implica convertir el decimal a una fracción y luego multiplicar las fracciones como de costumbre.
Conversión del Decimal a Fracción
Para convertir un decimal a una fracción, sigue estos pasos:
- Cuenta el número de dígitos después del punto decimal.
- Añade ceros al final del decimal para que tenga tantos dígitos como el número contado en el paso 1.
- El numerador es el número resultante del paso 2.
- El denominador es 1 seguido de tantos ceros como dígitos tenga el numerador.
Por ejemplo, para convertir 0,5 a una fracción:
- Hay un dígito después del punto decimal.
- Añadimos un cero al final: 0,50
- El numerador es 50.
- El denominador es 100.
Por lo tanto, 0,5 = 50/100.
Multiplicación de Fracciones
Una vez que el decimal se ha convertido a una fracción, se puede multiplicar por otra fracción de la forma habitual:
- Multiplica los numeradores.
- Multiplica los denominadores.
- Simplifica la fracción resultante, si es posible.
Por ejemplo, para multiplicar 1/2 por 0,5:
- Convertimos 0,5 a una fracción: 50/100
- Multiplicamos los numeradores: 1 x 50 = 50
- Multiplicamos los denominadores: 2 x 100 = 200
- La fracción resultante es 50/200.
- Simplificamos la fracción dividiendo el numerador y el denominador por 50: 50/200 = 1/4.
Por lo tanto, 1/2 x 0,5 = 1/4.
Casos Especiales en la Multiplicación de Fracciones
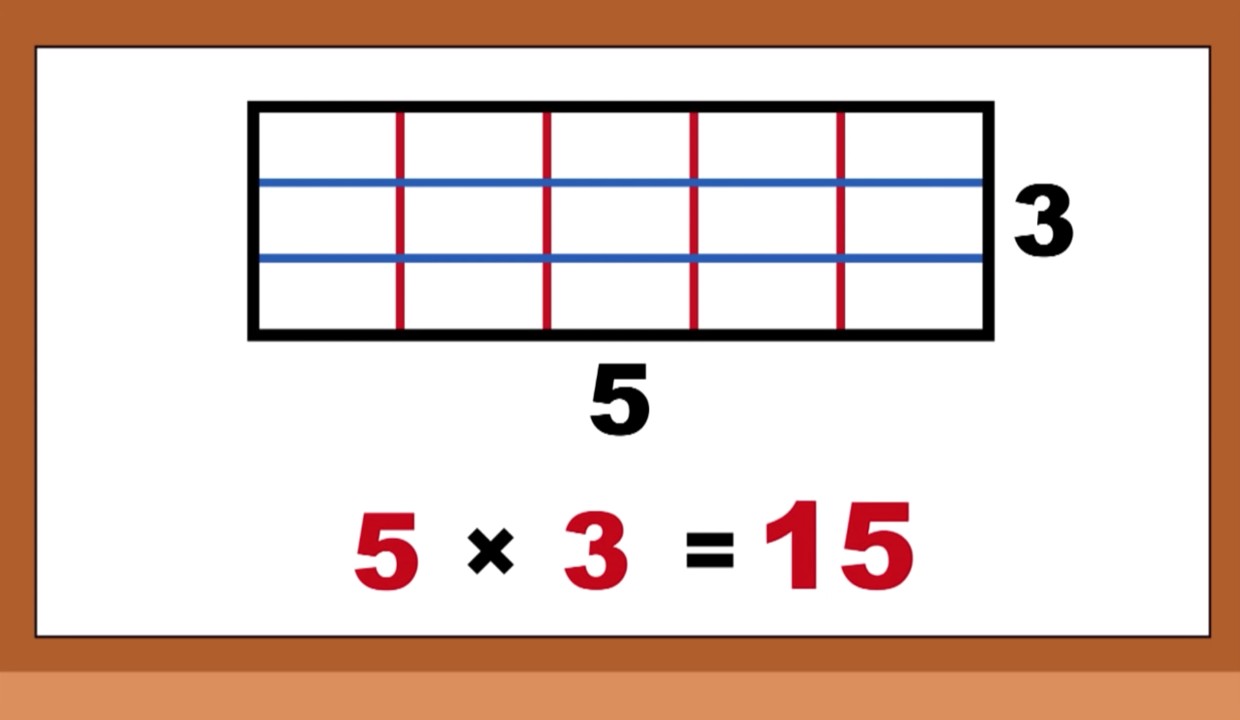
En ocasiones, al multiplicar fracciones, nos encontramos con casos especiales que requieren un manejo específico. Estos casos incluyen fracciones impropias y números mixtos.
Fracciones Impropias
Una fracción impropia es aquella cuyo numerador es mayor que su denominador. Al multiplicar fracciones impropias, el resultado será un número mixto. Para convertir una fracción impropia en un número mixto, dividimos el numerador entre el denominador. El cociente será la parte entera del número mixto, y el resto será el numerador de la fracción restante.Por
ejemplo:“`
/3 = 1 2/3
“`
Números Mixtos
Un número mixto es una combinación de un número entero y una fracción. Al multiplicar números mixtos, primero convertimos cada uno de ellos en una fracción impropia. Luego, multiplicamos las fracciones impropias y simplificamos el resultado.Por ejemplo:“`
1/2 x 3/4 = (5/2) x (3/4) = 15/8 = 1 7/8
“`
Aplicaciones de la Multiplicación de Fracciones en la Vida Real

La multiplicación de fracciones no es solo un concepto abstracto en matemáticas; tiene aplicaciones prácticas en diversas áreas de nuestra vida diaria. Desde compartir pizza hasta calcular costos, la multiplicación de fracciones nos ayuda a resolver problemas cotidianos con precisión.
En la Cocina
- Cuando sigues una receta, a menudo necesitas escalar o ajustar las cantidades de los ingredientes. La multiplicación de fracciones te permite duplicar, triplicar o reducir las cantidades originales.
- Al dividir una pizza o un pastel entre varias personas, la multiplicación de fracciones te ayuda a determinar la fracción que le corresponde a cada uno.
En las Compras
- Los descuentos y las ventas se expresan a menudo como fracciones. La multiplicación de fracciones te permite calcular el precio con descuento.
- Al comparar precios unitarios, la multiplicación de fracciones te ayuda a determinar cuál es la mejor oferta.
En la Construcción, Representacion Grafica De La Multiplicacion De Fracciones Para Niños
- Los planos arquitectónicos utilizan fracciones para representar escalas y dimensiones. La multiplicación de fracciones te permite convertir las medidas de los planos a las medidas reales.
- Al mezclar cemento u otros materiales de construcción, la multiplicación de fracciones te ayuda a determinar las proporciones correctas.
¡La multiplicación de fracciones ya no es un misterio! Con esta guía, los niños dominarán este concepto matemático fundamental con confianza y entusiasmo. ¡Prepárate para que sus mentes florezcan mientras descubren la belleza de las matemáticas a través de representaciones gráficas!
